#hide
with open('./data/original.json', 'r') as f:
data = json.load(f)
data = data["songs"]
def processMeasures(row):
measures = row["music"]["measures"]
chords = []
for measure in measures:
for chord in measure:
chords.append(chord)
return chords
for row in data:
if not row["music"]: continue
music = row["music"]
row["chords"] = processMeasures(row)
row["time_signature"] = music["timeSignature"]
row["original_measures"] = music["measures"]Introduction
In the context of jazz music, where improvisation is a focal component, jazz musicians look at a music notation called “charts”, which define a song in a loose format. In this project, using Tensorflow and LSTMs, we’ll build a model to produce a jazz “chart”.
Demos:
- deepharmony, a HuggingFace inference API built using the model built from this script
- MuseScore Plugins, the plugins built to integrate with the HuggingFace API.
Exploratory Data Analysis
The data comes from iRealPro’s repository of jazz standards. It has a fairly extensive collection of jazz music, with 1400 charts. There are other sources I could have pulled from, such as the real book series; but that would mean converting PDFs to a sequences of chords. Throughout the data analysis, I’ve used a Q&A format to explore the iRealPro dataset.
::: {.cell _cell_guid=‘b1076dfc-b9ad-4769-8c92-a6c4dae69d19’ _uuid=‘8f2839f25d086af736a60e9eeb907d3b93b6e0e5’ execution=‘{“iopub.execute_input”:“2022-11-08T03:30:38.537049Z”,“iopub.status.busy”:“2022-11-08T03:30:38.536364Z”,“iopub.status.idle”:“2022-11-08T03:30:38.559767Z”,“shell.execute_reply”:“2022-11-08T03:30:38.558565Z”,“shell.execute_reply.started”:“2022-11-08T03:30:38.536998Z”}’ trusted=‘true’ execution_count=2}
#hide
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import seaborn as sns
import tensorflow as tf
import matplotlib.pyplot as plt
from keras import Model
from keras.layers import Input, Dense, Bidirectional, Dropout, LSTM
import json
%matplotlib inline
TESTING = False:::
#hide
original = pd.DataFrame(data)
data = original.copy()
data.head()| title | composer | form | style | key | transpose | music | bpm | repeats | chords | time_signature | original_measures | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 9.20 Special 1 | Warren Earl | ABA | Medium Swing | C | None | {'measures': [['D9'], ['F-6'], ['D9'], ['F-6']... | 0 | 0 | [D9, F-6, D9, F-6, C, C7, B7, Bb7, A7, D9, G7,... | 44 | [[D9], [F-6], [D9], [F-6], [C], [C7, B7, Bb7, ... |
| 1 | 26-2 | Coltrane John | AABA | Medium Up Swing | F | None | {'measures': [['F^7', 'Ab7'], ['Db^7', 'E7'], ... | 0 | 0 | [F^7, Ab7, Db^7, E7, A^7, C7, C-7, F7, Bb^7, D... | 44 | [[F^7, Ab7], [Db^7, E7], [A^7, C7], [C-7, F7],... |
| 2 | 52nd Street Theme | Monk Thelonious | ABA | Up Tempo Swing | C | None | {'measures': [['C', 'A-7'], ['D-7', 'G7'], ['C... | 0 | 0 | [C, A-7, D-7, G7, C, A-7, D-7, G7, C, A-7, D-7... | 44 | [[C, A-7], [D-7, G7], [C, A-7], [D-7, G7], [C,... |
| 3 | 500 Miles High | Corea Chick | None | Bossa Nova | E- | None | {'measures': [['E-7'], ['E-7'], ['G-7'], ['G-7... | 0 | 0 | [E-7, E-7, G-7, G-7, Bb^7, Bb^7, Bh7, E7#9, A-... | 44 | [[E-7], [E-7], [G-7], [G-7], [Bb^7], [Bb^7], [... |
| 4 | 502 Blues | Rowles Jimmy | None | Waltz | A- | None | {'measures': [['A-7'], ['Db^7'], ['Bh7'], ['E7... | 0 | 0 | [A-7, Db^7, Bh7, E7#9, A-7, Db^7, Bh7, E7#9, C... | 34 | [[A-7], [Db^7], [Bh7], [E7#9], [A-7], [Db^7], ... |
NOTES = {
"Cb": 11,
"C": 0,
"C#": 1,
"Db": 1,
"D": 2,
"D#": 3,
"Eb": 3,
"E": 4,
"E#": 5,
"Fb": 4,
"F": 5,
"F#": 6,
"Gb": 6,
"G": 7,
"G#": 8,
"Ab": 8,
"A": 9,
"A#":10,
"Bb":10,
"B": 11,
"B#": 0,
}
max_length = max([len(seq) for seq in data.chords])
def encode_chords(chords):
res = []
for chord in chords:
if not chord: continue
c = []
if len(chord) > 2 and chord[0] + chord[1] in NOTES:
c.append(NOTES[chord[:2]])
else:
c.append(NOTES[chord[0]])
if "^" in chord:
c.append(1)
elif "-" in chord:
c.append(2)
elif "7" in chord:
c.append(3)
else:
c.append(1)
res.append(c)
padding = [[-1, -1] for _ in range(max_length - len(res))]
return res + padding
NUM_TO_NOTE = {
0: "C",
1: "Db",
2: "D",
3: "Eb",
4: "E",
5: "F",
6: "Gb",
7: "G",
8: "Ab",
9: "A",
10: "Bb",
11: "B",
-1: "",
}
NUM_TO_QUALITY = {
1: "^7",
2: "-7",
3: "7",
-1: "",
}
def decode_chords(chords):
res = []
for chord in chords:
res.append(NUM_TO_NOTE[chord[0]] + NUM_TO_QUALITY[chord[1]])
return res
def transpose_chords(chords, distance):
res = []
for chord in chords:
if chord[0] == -1:
res.append(chord)
else:
res.append([(chord[0] + distance) % 12, chord[1]])
return res
data["encoded_chords"] = data.chords.apply(encode_chords)Q: How many different time signatures exist and what does the distribution look like?
time_signatures = data.time_signature.value_counts().sort_values(ascending=False)
plt.title('Time Signatures')
sns.barplot(x=time_signatures.keys(), y=time_signatures.values)
print("Unique time signatures", data.time_signature.unique())Unique time signatures ['44' '34' '54' '64' None '24']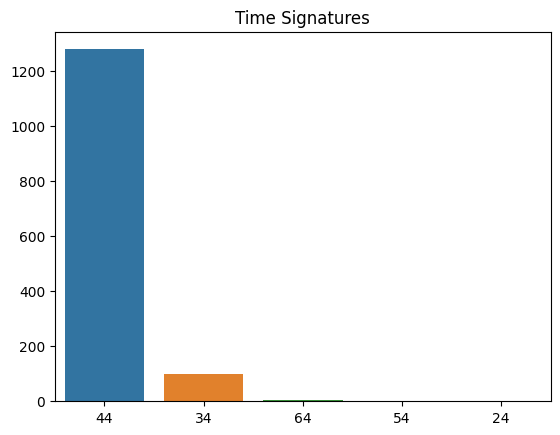
Q: What does the distribution of bars look like?
data["barCount"] = data.original_measures.apply(len)
data["barCount"].describe()count 1400.000000
mean 34.438571
std 12.923670
min 7.000000
25% 32.000000
50% 32.000000
75% 36.000000
max 122.000000
Name: barCount, dtype: float64bars = data.barCount.value_counts()
sns.displot(bars.keys(), kde=True)<seaborn.axisgrid.FacetGrid at 0x1b85669eb30>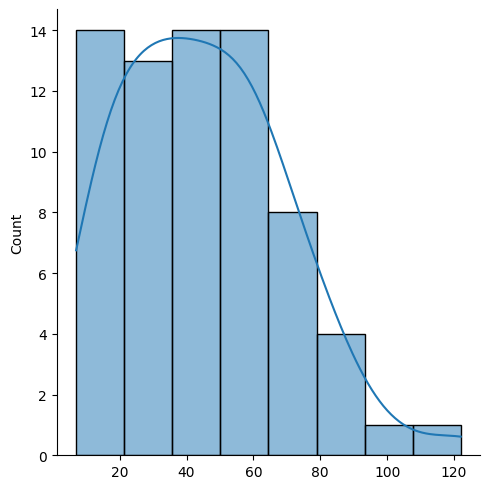
Q: What are the distribution of keys?
keys = data.key.value_counts().sort_values(ascending=False)
plt.title('Key Distributions')
sns.barplot(x=keys.keys(), y=keys.values)<AxesSubplot: title={'center': 'Key Distributions'}>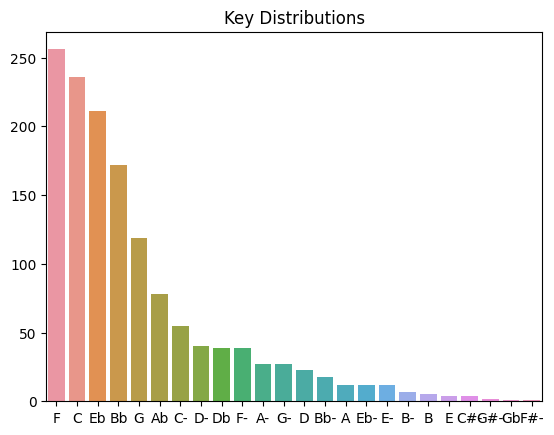
Q: What is the average count of chords in a song?
data["chordCounts"] = data.chords.apply(len)
data["chordCounts"].describe()count 1400.000000
mean 48.544286
std 19.562171
min 7.000000
25% 36.000000
50% 48.000000
75% 59.000000
max 224.000000
Name: chordCounts, dtype: float64We can see that there are some anomalies within the chord counts. From my personal knowledge, I know that a standard has around 32 bars. As an example; a standard can have 4 parts, AABA. With a single part containing 8 bars, or 32 measures total.
Q: How many 25s are there in a single song?
def count25s(chords):
count = 0
for i in range(1, len(chords)):
curr = chords[i]
prev = chords[i - 1]
if prev[1] == 2 and curr[1] == 3 and curr[0] - prev[0] == 5:
count += 1
return count
data["two_five_count"] = data.encoded_chords.map(count25s)
data.two_five_count.value_counts().sort_values(ascending=False).plot(kind='barh', xlabel='Number of Songs', ylabel='Number of 25s')<AxesSubplot: xlabel='Number of Songs', ylabel='Number of 25s'>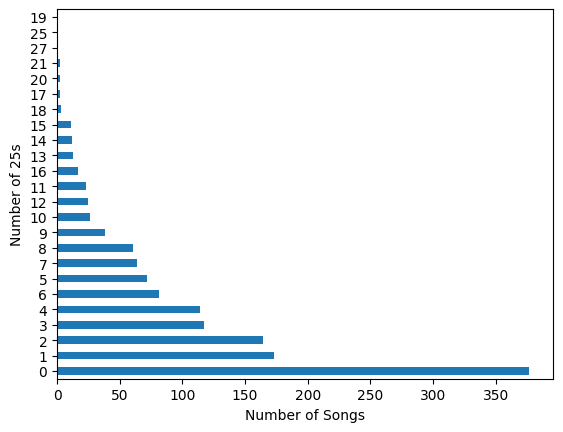
Which is really striking, because this would indicate that there are more than 250 songs without 25s. If a 25 chord progression is what we are looking for within our models, we should explore and train a model with a subset of the data that has a high number of 25s.
Let’s make a copy of data and remove songs that only have less than 5 25s.
data_25 = data.loc[data.two_five_count > 5]
data_25.two_five_count.value_counts().sort_values(ascending=False).plot(kind='barh', xlabel='Number of Songs', ylabel='Number of 25s')
data = data_25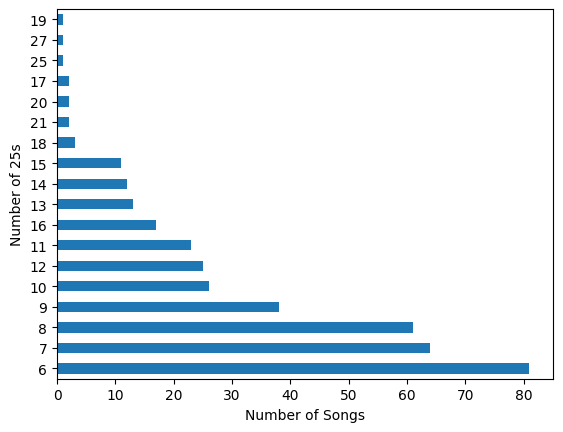
Q: What are the various form structures within a standard?
Some potential structures might be: AABA, ABAB, ABAC, AB, or None (Blues do not have repeating parts)
data.form.value_counts().sort_values(ascending=False).plot(kind='barh', xlabel='Count', ylabel='Form Types')<AxesSubplot: xlabel='Count', ylabel='Form Types'>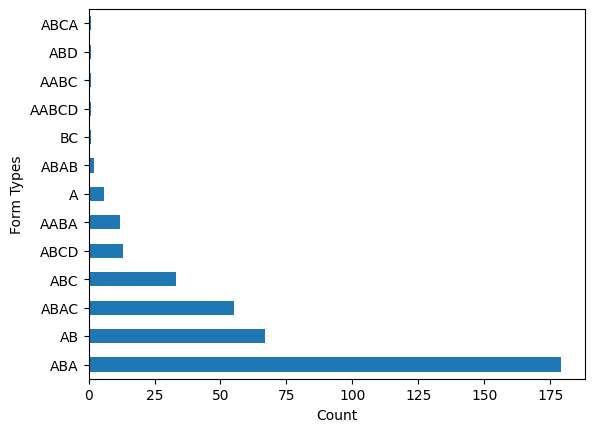
Refining the main hypothesis: Would the model be able to detect a form structure?
This was one piece of insight that could lead to a higher quality result, and therefore a better quality model, is to generate sequences of chords that represent parts of the song. Then, the model would be able to build a song structure such as AABA (A repeating three times, and B as the bridge).
Data Cleaning
Let’s delete the duplicate column “music”
data.drop(["music"], axis=1)| title | composer | form | style | key | transpose | bpm | repeats | chords | time_signature | original_measures | encoded_chords | barCount | chordCounts | two_five_count | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 26-2 | Coltrane John | AABA | Medium Up Swing | F | None | 0 | 0 | [F^7, Ab7, Db^7, E7, A^7, C7, C-7, F7, Bb^7, D... | 44 | [[F^7, Ab7], [Db^7, E7], [A^7, C7], [C-7, F7],... | [[5, 1], [8, 3], [1, 1], [4, 3], [9, 1], [0, 3... | 32 | 58 | 7 |
| 2 | 52nd Street Theme | Monk Thelonious | ABA | Up Tempo Swing | C | None | 0 | 0 | [C, A-7, D-7, G7, C, A-7, D-7, G7, C, A-7, D-7... | 44 | [[C, A-7], [D-7, G7], [C, A-7], [D-7, G7], [C,... | [[0, 1], [9, 2], [2, 2], [7, 3], [0, 1], [9, 2... | 32 | 53 | 9 |
| 5 | A Ballad 1 | Mulligan Gerry | ABA | Ballad | C | None | 0 | 0 | [D-7, G7, C^7, A-7, C#-7, F#7#9, B^7, E-7, A7b... | 44 | [[D-7, G7], [C^7, A-7], [C#-7, F#7#9], [B^7], ... | [[2, 2], [7, 3], [0, 1], [9, 2], [1, 2], [6, 3... | 46 | 93 | 27 |
| 7 | A Blossom Fell | Barnes-Cornelius | AB | Ballad | Bb | None | 0 | 0 | [Bb6, Bo, C-7, F7, F7#5, Bb6, Bb^7/D, Dbo, C-7... | 44 | [[Bb6, Bo], [C-7], [F7, F7#5], [Bb6], [Bb^7/D,... | [[10, 1], [11, 1], [0, 2], [5, 3], [5, 3], [10... | 20 | 37 | 6 |
| 10 | A Felicidade 1 | Jobim Antonio-Carlos | ABCD | Bossa Nova | A- | None | 0 | 0 | [C^7, A-7, C^7, A-7, C^7, C^7, E-7, B7b9, E-7,... | 44 | [[C^7, A-7], [C^7, A-7], [C^7], [C^7], [E-7], ... | [[0, 1], [9, 2], [0, 1], [9, 2], [0, 1], [0, 1... | 56 | 70 | 7 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 1389 | You're My Everything | Warren Harry | AB | Medium Swing | C | None | 0 | 0 | [A-7, G-7, C7, F#-7, B7, E-7, A7, D-7, D-7, G7... | 44 | [[A-7], [G-7, C7], [F#-7, B7], [E-7, A7], [D-7... | [[9, 2], [7, 2], [0, 3], [6, 2], [11, 3], [4, ... | 32 | 43 | 7 |
| 1392 | You're The Top 1 | Porter Cole | ABC | Medium Swing | Eb | None | 0 | 0 | [Eb^7, Eo7, F-7, Bb7, G-7, F#o7, G-7, C7, F-7,... | 44 | [[Eb^7, Eo7], [F-7, Bb7], [G-7, F#o7], [G-7, C... | [[3, 1], [4, 3], [5, 2], [10, 3], [7, 2], [6, ... | 48 | 72 | 10 |
| 1394 | Young And Foolish 1 | Hague Albert | ABAC | Ballad | C | None | 0 | 0 | [C^7, A-7, D-7, G7, C^7, G-7, C7, F^7, Eh7, A7... | 44 | [[C^7, A-7], [D-7, G7], [C^7], [G-7, C7], [F^7... | [[0, 1], [9, 2], [2, 2], [7, 3], [0, 1], [7, 2... | 32 | 47 | 7 |
| 1395 | Young At Heart | Richards Johnny | ABC | Ballad | Bb | None | 0 | 0 | [Bb^7, Bb^7, Dbo7, C-7, C-7, F7, C-7, F7, F7#5... | 44 | [[Bb^7], [Bb^7, Dbo7], [C-7], [C-7], [F7, C-7]... | [[10, 1], [10, 1], [1, 3], [0, 2], [0, 2], [5,... | 32 | 55 | 8 |
| 1397 | Zing Went The Strings Of My Heart 1 | Hanley James | ABA | Medium Swing | Eb | None | 0 | 0 | [Eb^7, Eb^7, C-7, C-7, F-7, F-7, Bb7, Bb7, Ab^... | 44 | [[Eb^7], [Eb^7], [C-7], [C-7], [F-7], [F-7], [... | [[3, 1], [3, 1], [0, 2], [0, 2], [5, 2], [5, 2... | 56 | 64 | 11 |
383 rows × 15 columns
Let’s transpose all of the data into a single key: C
def transpose_to_c(row):
curr_key_num = NOTES[row["key"].replace("-", "")]
row.encoded_chords = transpose_chords(row.encoded_chords, 12 - curr_key_num)
row.key = 'C'
return row
data = data.apply(transpose_to_c, axis='columns')And now that all of the keys are in C we’ll go ahead and transpose the data to various different keys
data["simplified_chords"] = data.encoded_chords.apply(decode_chords)
transposed = []
transposition_range = [3,8] if TESTING else range(1, 12)
for i in transposition_range:
print(i)
delta = data.copy()
delta.encoded_chords
delta["encoded_chords"] = data.encoded_chords.apply(lambda x: transpose_chords(x, i))
delta["key"] = NUM_TO_NOTE[i]
delta["simplified_chords"] = delta.encoded_chords.apply(decode_chords)
transposed.append(delta)1
2
3
4
5
6
7
8
9
10
11data = pd.concat([data, *transposed])data.key.value_counts()C 383
Db 383
D 383
Eb 383
E 383
F 383
Gb 383
G 383
Ab 383
A 383
Bb 383
B 383
Name: key, dtype: int64processed_chords = data.simplified_chords.map(lambda x: ' '.join(x))
print(processed_chords)
tokenizer = tf.keras.preprocessing.text.Tokenizer(num_words=None, split=' ', lower=False, filters='')
tokenizer.fit_on_texts(processed_chords)
vocab_size = len(tokenizer.word_counts) + 1
print('max_length', max_length)
print(tokenizer.word_index) # To see the dictionary
print('vocab_size', vocab_size)1 C^7 Eb7 Ab^7 B7 E^7 G7 G-7 C7 F^7 Ab7 Db^7 E7 ...
2 C^7 A-7 D-7 G7 C^7 A-7 D-7 G7 C^7 A-7 D-7 G7 C...
5 D-7 G7 C^7 A-7 Db-7 Gb7 B^7 E-7 A7 Gb-7 B7 E-7...
7 C^7 Db^7 D-7 G7 G7 C^7 C^7 Eb^7 D-7 G7 D-7 G7 ...
10 Eb^7 C-7 Eb^7 C-7 Eb^7 Eb^7 G-7 D7 G-7 C7 F-7 ...
...
1389 Ab-7 Gb-7 B7 F-7 Bb7 Eb-7 Ab7 Db-7 Db-7 Gb7 E^...
1392 B^7 C7 Db-7 Gb7 Eb-7 D7 Eb-7 Ab7 Db-7 Db-7 Gb7...
1394 B^7 Ab-7 Db-7 Gb7 B^7 Gb-7 B7 E^7 Eb7 Ab7 Db-7...
1395 B^7 B^7 D7 Db-7 Db-7 Gb7 Db-7 Gb7 Gb7 B^7 B^7 ...
1397 B^7 B^7 Ab-7 Ab-7 Db-7 Db-7 Gb7 Gb7 E^7 E^7 E-...
Name: simplified_chords, Length: 4596, dtype: object
max_length 224
{'Eb7': 1, 'B7': 2, 'G7': 3, 'C7': 4, 'Ab7': 5, 'E7': 6, 'D7': 7, 'Gb7': 8, 'A7': 9, 'F7': 10, 'Bb7': 11, 'Db7': 12, 'G-7': 13, 'A-7': 14, 'D-7': 15, 'B-7': 16, 'Bb-7': 17, 'Db-7': 18, 'E-7': 19, 'Gb-7': 20, 'F-7': 21, 'Eb-7': 22, 'C-7': 23, 'Ab-7': 24, 'C^7': 25, 'Ab^7': 26, 'E^7': 27, 'F^7': 28, 'Db^7': 29, 'A^7': 30, 'B^7': 31, 'D^7': 32, 'Eb^7': 33, 'Bb^7': 34, 'G^7': 35, 'Gb^7': 36}
vocab_size 37chords_int = []
for seq in processed_chords:
seq_int = np.zeros(max_length)
tokenized = tokenizer.texts_to_sequences(seq.split(" "))
with_zeros = np.zeros(len(tokenized))
for idx, token in enumerate(tokenized):
if len(token):
seq_int[idx] = token[0]
chords_int.append(seq_int)chords = tf.constant(chords_int)
dataset = tf.data.Dataset.from_tensor_slices(chords)
def decode(numpy_array):
total = []
for i in numpy_array:
total.append([i])
return tokenizer.sequences_to_texts(total)
for i in dataset.take(1):
print(decode(i.numpy()))['C^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'G-7', 'C7', 'F^7', 'Ab7', 'Db^7', 'E7', 'A-7', 'D7', 'D-7', 'G7', 'C^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'G-7', 'C7', 'F^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'C^7', 'G-7', 'C7', 'B-7', 'E7', 'A^7', 'C7', 'F^7', 'Bb-7', 'Eb7', 'Ab^7', 'D-7', 'G7', 'C^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'G-7', 'C7', 'F^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'C^7', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '']def split_input_target(chunk):
input = chunk[:-1]
target = chunk[1:]
return input, target
dataset = dataset.map(split_input_target)for input_example, target_example in dataset.take(1):
print('Input data original: ', len(input_example.numpy()), input_example.numpy())
print ('Input data: ', decode(input_example.numpy()))
print ('Target data:', decode(target_example.numpy()))Input data original: 223 [25. 1. 26. 2. 27. 3. 13. 4. 28. 5. 29. 6. 14. 7. 15. 3. 25. 1.
26. 2. 27. 3. 13. 4. 28. 1. 26. 2. 27. 3. 25. 13. 4. 16. 6. 30.
4. 28. 17. 1. 26. 15. 3. 25. 1. 26. 2. 27. 3. 13. 4. 28. 1. 26.
2. 27. 3. 25. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0.]
Input data: ['C^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'G-7', 'C7', 'F^7', 'Ab7', 'Db^7', 'E7', 'A-7', 'D7', 'D-7', 'G7', 'C^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'G-7', 'C7', 'F^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'C^7', 'G-7', 'C7', 'B-7', 'E7', 'A^7', 'C7', 'F^7', 'Bb-7', 'Eb7', 'Ab^7', 'D-7', 'G7', 'C^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'G-7', 'C7', 'F^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'C^7', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '']
Target data: ['Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'G-7', 'C7', 'F^7', 'Ab7', 'Db^7', 'E7', 'A-7', 'D7', 'D-7', 'G7', 'C^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'G-7', 'C7', 'F^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'C^7', 'G-7', 'C7', 'B-7', 'E7', 'A^7', 'C7', 'F^7', 'Bb-7', 'Eb7', 'Ab^7', 'D-7', 'G7', 'C^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'G-7', 'C7', 'F^7', 'Eb7', 'Ab^7', 'B7', 'E^7', 'G7', 'C^7', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '', '']Building the Model
Now that we’ve explored and cleaned the data, let’s start constructing our model using an LSTM architecture.
# Batch size
BATCH_SIZE = 64
# Buffer size to shuffle the dataset
# (TF data is designed to work with possibly infinite sequences,
# so it doesn't attempt to shuffle the entire sequence in memory. Instead,
# it maintains a buffer in which it shuffles elements).
BUFFER_SIZE = 10000
def shuffleBatch(ds):
return ds.shuffle(BUFFER_SIZE).batch(BATCH_SIZE, drop_remainder=True)
def get_dataset_partitions(ds, ds_size, train_split=0.8, val_split=0.1, test_split=0.1, shuffle=True, shuffle_size=10000):
assert (train_split + test_split + val_split) == 1
if shuffle:
ds = ds.shuffle(shuffle_size, seed=12)
train_size = int(train_split * ds_size)
val_size = int(val_split * ds_size)
train_ds = ds.take(train_size)
val_ds = ds.skip(train_size).take(val_size)
test_ds = ds.skip(train_size).skip(val_size)
return train_ds, val_ds, test_ds
ds = shuffleBatch(dataset)
train_ds, val_ds, test_ds = get_dataset_partitions(dataset, len(chords_int))
train_ds, val_ds, test_ds = shuffleBatch(train_ds), shuffleBatch(val_ds), shuffleBatch(test_ds)
ds<BatchDataset element_spec=(TensorSpec(shape=(64, 223), dtype=tf.float64, name=None), TensorSpec(shape=(64, 223), dtype=tf.float64, name=None))>def build_model(vocab_size, embedding_dim, rnn_units, batch_size):
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim,
batch_input_shape=[batch_size, None]),
tf.keras.layers.LSTM(units=rnn_units, return_sequences=True),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.LSTM(units=rnn_units, return_sequences=True),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.LSTM(units=rnn_units, return_sequences=True),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(vocab_size),
tf.keras.layers.Activation('softmax')
])
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=1e-3), loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.summary()
return modelif TESTING:
embedding_dim = 50
rnn_units = 50
else:
embedding_dim = 400
rnn_units = 400
model = build_model(
vocab_size = len(tokenizer.word_counts) + 1,
embedding_dim=embedding_dim,
rnn_units=rnn_units,
batch_size=BATCH_SIZE
)Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
embedding (Embedding) (64, None, 400) 14800
lstm (LSTM) (64, None, 400) 1281600
dropout (Dropout) (64, None, 400) 0
lstm_1 (LSTM) (64, None, 400) 1281600
dropout_1 (Dropout) (64, None, 400) 0
lstm_2 (LSTM) (64, None, 400) 1281600
dropout_2 (Dropout) (64, None, 400) 0
dense (Dense) (64, None, 37) 14837
activation (Activation) (64, None, 37) 0
=================================================================
Total params: 3,874,437
Trainable params: 3,874,437
Non-trainable params: 0
_________________________________________________________________# Directory where the checkpoints will be saved
checkpoint_dir = './training_checkpoints'
# Name of the checkpoint files
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt_{epoch}")
checkpoint_callback=tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_prefix,
save_weights_only=True)from tensorflow.keras.callbacks import EarlyStopping
early_stopping = EarlyStopping(
min_delta=0.001, # minimium amount of change to count as an improvement
patience=4, # how many epochs to wait before stopping
restore_best_weights=True,
)
if TESTING:
epochs = 3
else:
epochs = 200
history = model.fit(train_ds,
epochs=epochs,
validation_data=val_ds,
callbacks=[checkpoint_callback, early_stopping],
)Epoch 1/200
57/57 [==============================] - 16s 145ms/step - loss: 1.0627 - accuracy: 0.7338 - val_loss: 0.8963 - val_accuracy: 0.7546
Epoch 2/200
57/57 [==============================] - 7s 116ms/step - loss: 0.8511 - accuracy: 0.7614 - val_loss: 0.8091 - val_accuracy: 0.7702
Epoch 3/200
57/57 [==============================] - 7s 124ms/step - loss: 0.7831 - accuracy: 0.7750 - val_loss: 0.7549 - val_accuracy: 0.7801
Epoch 4/200
57/57 [==============================] - 7s 115ms/step - loss: 0.7582 - accuracy: 0.7803 - val_loss: 0.7420 - val_accuracy: 0.7898
Epoch 5/200
57/57 [==============================] - 7s 122ms/step - loss: 0.7227 - accuracy: 0.7980 - val_loss: 0.7004 - val_accuracy: 0.8102
Epoch 6/200
57/57 [==============================] - 7s 123ms/step - loss: 0.6820 - accuracy: 0.8153 - val_loss: 0.6155 - val_accuracy: 0.8356
Epoch 7/200
57/57 [==============================] - 7s 121ms/step - loss: 0.6320 - accuracy: 0.8348 - val_loss: 0.6011 - val_accuracy: 0.8455
Epoch 8/200
57/57 [==============================] - 7s 115ms/step - loss: 0.5828 - accuracy: 0.8515 - val_loss: 0.5497 - val_accuracy: 0.8597
Epoch 9/200
57/57 [==============================] - 7s 123ms/step - loss: 0.5549 - accuracy: 0.8583 - val_loss: 0.5268 - val_accuracy: 0.8642
Epoch 10/200
57/57 [==============================] - 7s 121ms/step - loss: 0.5318 - accuracy: 0.8631 - val_loss: 0.5151 - val_accuracy: 0.8659
Epoch 11/200
57/57 [==============================] - 6s 112ms/step - loss: 0.5205 - accuracy: 0.8657 - val_loss: 0.5031 - val_accuracy: 0.8690
Epoch 12/200
57/57 [==============================] - 7s 117ms/step - loss: 0.5072 - accuracy: 0.8678 - val_loss: 0.4808 - val_accuracy: 0.8737
Epoch 13/200
57/57 [==============================] - 7s 121ms/step - loss: 0.4914 - accuracy: 0.8716 - val_loss: 0.4730 - val_accuracy: 0.8753
Epoch 14/200
57/57 [==============================] - 7s 124ms/step - loss: 0.4874 - accuracy: 0.8723 - val_loss: 0.4644 - val_accuracy: 0.8775
Epoch 15/200
57/57 [==============================] - 7s 122ms/step - loss: 0.4771 - accuracy: 0.8743 - val_loss: 0.4509 - val_accuracy: 0.8789
Epoch 16/200
57/57 [==============================] - 7s 116ms/step - loss: 0.4716 - accuracy: 0.8755 - val_loss: 0.4422 - val_accuracy: 0.8818
Epoch 17/200
57/57 [==============================] - 7s 122ms/step - loss: 0.4606 - accuracy: 0.8778 - val_loss: 0.4266 - val_accuracy: 0.8850
Epoch 18/200
57/57 [==============================] - 6s 112ms/step - loss: 0.4543 - accuracy: 0.8790 - val_loss: 0.4270 - val_accuracy: 0.8848
Epoch 19/200
57/57 [==============================] - 6s 111ms/step - loss: 0.4460 - accuracy: 0.8812 - val_loss: 0.4335 - val_accuracy: 0.8835
Epoch 20/200
57/57 [==============================] - 6s 110ms/step - loss: 0.4390 - accuracy: 0.8826 - val_loss: 0.4108 - val_accuracy: 0.8881
Epoch 21/200
57/57 [==============================] - 7s 115ms/step - loss: 0.4351 - accuracy: 0.8835 - val_loss: 0.3895 - val_accuracy: 0.8938
Epoch 22/200
57/57 [==============================] - 6s 108ms/step - loss: 0.4277 - accuracy: 0.8850 - val_loss: 0.3912 - val_accuracy: 0.8939
Epoch 23/200
57/57 [==============================] - 6s 112ms/step - loss: 0.4189 - accuracy: 0.8870 - val_loss: 0.3686 - val_accuracy: 0.9000
Epoch 24/200
57/57 [==============================] - 7s 113ms/step - loss: 0.4144 - accuracy: 0.8880 - val_loss: 0.3856 - val_accuracy: 0.8940
Epoch 25/200
57/57 [==============================] - 6s 110ms/step - loss: 0.4086 - accuracy: 0.8893 - val_loss: 0.3761 - val_accuracy: 0.8978
Epoch 26/200
57/57 [==============================] - 7s 115ms/step - loss: 0.4013 - accuracy: 0.8911 - val_loss: 0.3603 - val_accuracy: 0.8998
Epoch 27/200
57/57 [==============================] - 6s 106ms/step - loss: 0.3934 - accuracy: 0.8927 - val_loss: 0.3590 - val_accuracy: 0.9009
Epoch 28/200
57/57 [==============================] - 6s 103ms/step - loss: 0.3903 - accuracy: 0.8933 - val_loss: 0.3612 - val_accuracy: 0.9002
Epoch 29/200
57/57 [==============================] - 6s 112ms/step - loss: 0.3804 - accuracy: 0.8957 - val_loss: 0.3345 - val_accuracy: 0.9081
Epoch 30/200
57/57 [==============================] - 6s 109ms/step - loss: 0.3729 - accuracy: 0.8976 - val_loss: 0.3353 - val_accuracy: 0.9075
Epoch 31/200
57/57 [==============================] - 6s 110ms/step - loss: 0.3669 - accuracy: 0.8989 - val_loss: 0.3300 - val_accuracy: 0.9069
Epoch 32/200
57/57 [==============================] - 6s 107ms/step - loss: 0.3625 - accuracy: 0.8996 - val_loss: 0.3093 - val_accuracy: 0.9125
Epoch 33/200
57/57 [==============================] - 6s 106ms/step - loss: 0.3546 - accuracy: 0.9015 - val_loss: 0.3110 - val_accuracy: 0.9128
Epoch 34/200
57/57 [==============================] - 6s 110ms/step - loss: 0.3496 - accuracy: 0.9027 - val_loss: 0.3002 - val_accuracy: 0.9166
Epoch 35/200
57/57 [==============================] - 6s 107ms/step - loss: 0.3411 - accuracy: 0.9048 - val_loss: 0.3039 - val_accuracy: 0.9141
Epoch 36/200
57/57 [==============================] - 6s 113ms/step - loss: 0.3335 - accuracy: 0.9066 - val_loss: 0.2799 - val_accuracy: 0.9211
Epoch 37/200
57/57 [==============================] - 7s 114ms/step - loss: 0.3321 - accuracy: 0.9068 - val_loss: 0.2839 - val_accuracy: 0.9209
Epoch 38/200
57/57 [==============================] - 6s 109ms/step - loss: 0.3248 - accuracy: 0.9086 - val_loss: 0.2705 - val_accuracy: 0.9233
Epoch 39/200
57/57 [==============================] - 6s 107ms/step - loss: 0.3177 - accuracy: 0.9105 - val_loss: 0.2634 - val_accuracy: 0.9260
Epoch 40/200
57/57 [==============================] - 7s 115ms/step - loss: 0.3122 - accuracy: 0.9115 - val_loss: 0.2558 - val_accuracy: 0.9279
Epoch 41/200
57/57 [==============================] - 6s 111ms/step - loss: 0.3049 - accuracy: 0.9133 - val_loss: 0.2506 - val_accuracy: 0.9287
Epoch 42/200
57/57 [==============================] - 6s 110ms/step - loss: 0.3016 - accuracy: 0.9141 - val_loss: 0.2390 - val_accuracy: 0.9323
Epoch 43/200
57/57 [==============================] - 6s 109ms/step - loss: 0.2933 - accuracy: 0.9163 - val_loss: 0.2337 - val_accuracy: 0.9332
Epoch 44/200
57/57 [==============================] - 6s 106ms/step - loss: 0.2878 - accuracy: 0.9178 - val_loss: 0.2269 - val_accuracy: 0.9353
Epoch 45/200
57/57 [==============================] - 6s 112ms/step - loss: 0.2820 - accuracy: 0.9189 - val_loss: 0.2196 - val_accuracy: 0.9378
Epoch 46/200
57/57 [==============================] - 7s 119ms/step - loss: 0.2758 - accuracy: 0.9202 - val_loss: 0.2193 - val_accuracy: 0.9383
Epoch 47/200
57/57 [==============================] - 7s 114ms/step - loss: 0.2706 - accuracy: 0.9217 - val_loss: 0.2078 - val_accuracy: 0.9413
Epoch 48/200
57/57 [==============================] - 6s 109ms/step - loss: 0.2652 - accuracy: 0.9228 - val_loss: 0.2009 - val_accuracy: 0.9434
Epoch 49/200
57/57 [==============================] - 6s 112ms/step - loss: 0.2597 - accuracy: 0.9246 - val_loss: 0.2000 - val_accuracy: 0.9435
Epoch 50/200
57/57 [==============================] - 6s 109ms/step - loss: 0.2560 - accuracy: 0.9254 - val_loss: 0.1933 - val_accuracy: 0.9449
Epoch 51/200
57/57 [==============================] - 6s 109ms/step - loss: 0.2499 - accuracy: 0.9267 - val_loss: 0.1796 - val_accuracy: 0.9491
Epoch 52/200
57/57 [==============================] - 6s 110ms/step - loss: 0.2444 - accuracy: 0.9285 - val_loss: 0.1744 - val_accuracy: 0.9507
Epoch 53/200
57/57 [==============================] - 6s 113ms/step - loss: 0.2386 - accuracy: 0.9300 - val_loss: 0.1712 - val_accuracy: 0.9519
Epoch 54/200
57/57 [==============================] - 6s 107ms/step - loss: 0.2358 - accuracy: 0.9307 - val_loss: 0.1656 - val_accuracy: 0.9536
Epoch 55/200
57/57 [==============================] - 6s 113ms/step - loss: 0.2305 - accuracy: 0.9321 - val_loss: 0.1630 - val_accuracy: 0.9540
Epoch 56/200
57/57 [==============================] - 6s 111ms/step - loss: 0.2264 - accuracy: 0.9329 - val_loss: 0.1612 - val_accuracy: 0.9549
Epoch 57/200
57/57 [==============================] - 6s 110ms/step - loss: 0.2222 - accuracy: 0.9343 - val_loss: 0.1542 - val_accuracy: 0.9575
Epoch 58/200
57/57 [==============================] - 6s 112ms/step - loss: 0.2184 - accuracy: 0.9350 - val_loss: 0.1450 - val_accuracy: 0.9589
Epoch 59/200
57/57 [==============================] - 6s 107ms/step - loss: 0.2135 - accuracy: 0.9366 - val_loss: 0.1409 - val_accuracy: 0.9605
Epoch 60/200
57/57 [==============================] - 7s 114ms/step - loss: 0.2099 - accuracy: 0.9373 - val_loss: 0.1296 - val_accuracy: 0.9635
Epoch 61/200
57/57 [==============================] - 6s 109ms/step - loss: 0.2056 - accuracy: 0.9385 - val_loss: 0.1361 - val_accuracy: 0.9621
Epoch 62/200
57/57 [==============================] - 7s 113ms/step - loss: 0.2025 - accuracy: 0.9396 - val_loss: 0.1273 - val_accuracy: 0.9658
Epoch 63/200
57/57 [==============================] - 7s 114ms/step - loss: 0.1988 - accuracy: 0.9401 - val_loss: 0.1279 - val_accuracy: 0.9655
Epoch 64/200
57/57 [==============================] - 6s 108ms/step - loss: 0.1945 - accuracy: 0.9415 - val_loss: 0.1259 - val_accuracy: 0.9655
Epoch 65/200
57/57 [==============================] - 7s 114ms/step - loss: 0.1934 - accuracy: 0.9416 - val_loss: 0.1161 - val_accuracy: 0.9682
Epoch 66/200
57/57 [==============================] - 6s 112ms/step - loss: 0.1895 - accuracy: 0.9426 - val_loss: 0.1153 - val_accuracy: 0.9680
Epoch 67/200
57/57 [==============================] - 6s 111ms/step - loss: 0.1862 - accuracy: 0.9434 - val_loss: 0.1109 - val_accuracy: 0.9697
Epoch 68/200
57/57 [==============================] - 6s 113ms/step - loss: 0.1835 - accuracy: 0.9443 - val_loss: 0.1073 - val_accuracy: 0.9706
Epoch 69/200
57/57 [==============================] - 6s 111ms/step - loss: 0.1802 - accuracy: 0.9454 - val_loss: 0.1077 - val_accuracy: 0.9706
Epoch 70/200
57/57 [==============================] - 6s 112ms/step - loss: 0.1770 - accuracy: 0.9462 - val_loss: 0.1000 - val_accuracy: 0.9738
Epoch 71/200
57/57 [==============================] - 6s 112ms/step - loss: 0.1749 - accuracy: 0.9465 - val_loss: 0.1010 - val_accuracy: 0.9731
Epoch 72/200
57/57 [==============================] - 6s 107ms/step - loss: 0.1720 - accuracy: 0.9474 - val_loss: 0.0957 - val_accuracy: 0.9745
Epoch 73/200
57/57 [==============================] - 6s 111ms/step - loss: 0.1681 - accuracy: 0.9487 - val_loss: 0.0938 - val_accuracy: 0.9752
Epoch 74/200
57/57 [==============================] - 6s 111ms/step - loss: 0.1668 - accuracy: 0.9488 - val_loss: 0.0919 - val_accuracy: 0.9750
Epoch 75/200
57/57 [==============================] - 7s 115ms/step - loss: 0.1634 - accuracy: 0.9499 - val_loss: 0.0861 - val_accuracy: 0.9777
Epoch 76/200
57/57 [==============================] - 6s 113ms/step - loss: 0.1616 - accuracy: 0.9502 - val_loss: 0.0868 - val_accuracy: 0.9774
Epoch 77/200
57/57 [==============================] - 6s 109ms/step - loss: 0.1596 - accuracy: 0.9509 - val_loss: 0.0842 - val_accuracy: 0.9781
Epoch 78/200
57/57 [==============================] - 6s 111ms/step - loss: 0.1580 - accuracy: 0.9513 - val_loss: 0.0817 - val_accuracy: 0.9787
Epoch 79/200
57/57 [==============================] - 6s 110ms/step - loss: 0.1559 - accuracy: 0.9519 - val_loss: 0.0814 - val_accuracy: 0.9792
Epoch 80/200
57/57 [==============================] - 6s 109ms/step - loss: 0.1523 - accuracy: 0.9530 - val_loss: 0.0778 - val_accuracy: 0.9796
Epoch 81/200
57/57 [==============================] - 6s 106ms/step - loss: 0.1514 - accuracy: 0.9533 - val_loss: 0.0771 - val_accuracy: 0.9802
Epoch 82/200
57/57 [==============================] - 6s 109ms/step - loss: 0.1508 - accuracy: 0.9533 - val_loss: 0.0762 - val_accuracy: 0.9802
Epoch 83/200
57/57 [==============================] - 7s 116ms/step - loss: 0.1478 - accuracy: 0.9541 - val_loss: 0.0722 - val_accuracy: 0.9820
Epoch 84/200
57/57 [==============================] - 6s 108ms/step - loss: 0.1451 - accuracy: 0.9550 - val_loss: 0.0720 - val_accuracy: 0.9814
Epoch 85/200
57/57 [==============================] - 7s 116ms/step - loss: 0.1446 - accuracy: 0.9551 - val_loss: 0.0715 - val_accuracy: 0.9819
Epoch 86/200
57/57 [==============================] - 6s 110ms/step - loss: 0.1429 - accuracy: 0.9558 - val_loss: 0.0681 - val_accuracy: 0.9826
Epoch 87/200
57/57 [==============================] - 6s 110ms/step - loss: 0.1406 - accuracy: 0.9563 - val_loss: 0.0686 - val_accuracy: 0.9823
Epoch 88/200
57/57 [==============================] - 6s 113ms/step - loss: 0.1392 - accuracy: 0.9567 - val_loss: 0.0629 - val_accuracy: 0.9843
Epoch 89/200
57/57 [==============================] - 6s 109ms/step - loss: 0.1384 - accuracy: 0.9571 - val_loss: 0.0640 - val_accuracy: 0.9837
Epoch 90/200
57/57 [==============================] - 6s 110ms/step - loss: 0.1357 - accuracy: 0.9578 - val_loss: 0.0625 - val_accuracy: 0.9840
Epoch 91/200
57/57 [==============================] - 6s 109ms/step - loss: 0.1342 - accuracy: 0.9583 - val_loss: 0.0611 - val_accuracy: 0.9843
Epoch 92/200
57/57 [==============================] - 6s 111ms/step - loss: 0.1345 - accuracy: 0.9579 - val_loss: 0.0611 - val_accuracy: 0.9845
Epoch 93/200
57/57 [==============================] - 7s 117ms/step - loss: 0.1319 - accuracy: 0.9589 - val_loss: 0.0601 - val_accuracy: 0.9852
Epoch 94/200
57/57 [==============================] - 6s 110ms/step - loss: 0.1305 - accuracy: 0.9590 - val_loss: 0.0568 - val_accuracy: 0.9856
Epoch 95/200
57/57 [==============================] - 6s 112ms/step - loss: 0.1294 - accuracy: 0.9596 - val_loss: 0.0569 - val_accuracy: 0.9857
Epoch 96/200
57/57 [==============================] - 6s 109ms/step - loss: 0.1274 - accuracy: 0.9601 - val_loss: 0.0570 - val_accuracy: 0.9856
Epoch 97/200
57/57 [==============================] - 6s 108ms/step - loss: 0.1275 - accuracy: 0.9600 - val_loss: 0.0556 - val_accuracy: 0.9859
Epoch 98/200
57/57 [==============================] - 6s 113ms/step - loss: 0.1256 - accuracy: 0.9608 - val_loss: 0.0566 - val_accuracy: 0.9857
Epoch 99/200
57/57 [==============================] - 6s 110ms/step - loss: 0.1245 - accuracy: 0.9610 - val_loss: 0.0541 - val_accuracy: 0.9862
Epoch 100/200
57/57 [==============================] - 7s 114ms/step - loss: 0.1239 - accuracy: 0.9612 - val_loss: 0.0542 - val_accuracy: 0.9860
Epoch 101/200
57/57 [==============================] - 6s 110ms/step - loss: 0.1226 - accuracy: 0.9618 - val_loss: 0.0530 - val_accuracy: 0.9863
Epoch 102/200
57/57 [==============================] - 6s 112ms/step - loss: 0.1220 - accuracy: 0.9619 - val_loss: 0.0505 - val_accuracy: 0.9875
Epoch 103/200
57/57 [==============================] - 6s 112ms/step - loss: 0.1197 - accuracy: 0.9623 - val_loss: 0.0509 - val_accuracy: 0.9869
Epoch 104/200
57/57 [==============================] - 7s 114ms/step - loss: 0.1192 - accuracy: 0.9626 - val_loss: 0.0505 - val_accuracy: 0.9871
Epoch 105/200
57/57 [==============================] - 6s 112ms/step - loss: 0.1180 - accuracy: 0.9630 - val_loss: 0.0514 - val_accuracy: 0.9871
Epoch 106/200
57/57 [==============================] - 6s 109ms/step - loss: 0.1172 - accuracy: 0.9633 - val_loss: 0.0487 - val_accuracy: 0.9878
Epoch 107/200
57/57 [==============================] - 6s 109ms/step - loss: 0.1158 - accuracy: 0.9634 - val_loss: 0.0478 - val_accuracy: 0.9878
Epoch 108/200
57/57 [==============================] - 7s 116ms/step - loss: 0.1151 - accuracy: 0.9638 - val_loss: 0.0485 - val_accuracy: 0.9875
Epoch 109/200
57/57 [==============================] - 6s 109ms/step - loss: 0.1152 - accuracy: 0.9640 - val_loss: 0.0471 - val_accuracy: 0.9882
Epoch 110/200
57/57 [==============================] - 6s 112ms/step - loss: 0.1137 - accuracy: 0.9642 - val_loss: 0.0487 - val_accuracy: 0.9878
Epoch 111/200
57/57 [==============================] - 6s 110ms/step - loss: 0.1129 - accuracy: 0.9647 - val_loss: 0.0461 - val_accuracy: 0.9885
Epoch 112/200
57/57 [==============================] - 6s 113ms/step - loss: 0.1124 - accuracy: 0.9647 - val_loss: 0.0456 - val_accuracy: 0.9885
Epoch 113/200
57/57 [==============================] - 6s 112ms/step - loss: 0.1114 - accuracy: 0.9649 - val_loss: 0.0449 - val_accuracy: 0.9887
Epoch 114/200
57/57 [==============================] - 6s 108ms/step - loss: 0.1109 - accuracy: 0.9650 - val_loss: 0.0446 - val_accuracy: 0.9887
Epoch 115/200
57/57 [==============================] - 7s 114ms/step - loss: 0.1097 - accuracy: 0.9655 - val_loss: 0.0447 - val_accuracy: 0.9887
Epoch 116/200
57/57 [==============================] - 7s 114ms/step - loss: 0.1085 - accuracy: 0.9659 - val_loss: 0.0438 - val_accuracy: 0.9885
Epoch 117/200
57/57 [==============================] - 6s 113ms/step - loss: 0.1089 - accuracy: 0.9656 - val_loss: 0.0446 - val_accuracy: 0.9885
Epoch 118/200
57/57 [==============================] - 6s 109ms/step - loss: 0.1085 - accuracy: 0.9660 - val_loss: 0.0436 - val_accuracy: 0.9888
Epoch 119/200
57/57 [==============================] - 7s 116ms/step - loss: 0.1069 - accuracy: 0.9665 - val_loss: 0.0433 - val_accuracy: 0.9891
Epoch 120/200
57/57 [==============================] - 6s 113ms/step - loss: 0.1064 - accuracy: 0.9666 - val_loss: 0.0441 - val_accuracy: 0.9886Evaluation
Now that the model is trained, let’s see how it fares.
score = model.evaluate(test_ds, batch_size=BATCH_SIZE, verbose=0)
print('Evaluation With Test Dataset:', score[1])Evaluation With Test Dataset: 0.9887492060661316import joblib
model.save('./output/model.h5')
joblib.dump(tokenizer, './output/tokenizer.pkl')['./output/tokenizer.pkl']history_df = pd.DataFrame(history.history)
history_df.loc[:, ['loss', 'val_loss']].plot();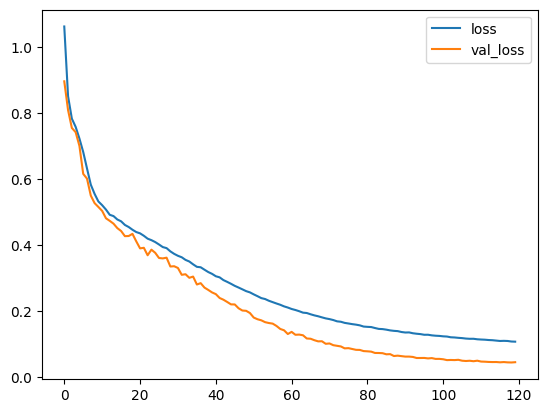
Looks like the model is learning fairly well. Let’s build about a hundred songs and see if there are 25 chord progression patterns generated.
def generate_chord(model, start):
# Evaluation step (generating text using the learned model)
# Number of characters to generate
num_generate = 100
# Converting our start string to numbers (vectorizing)
input_eval = [start]
input_eval = tf.expand_dims(input_eval, 0)
# Empty string to store our results
chords = [start]
# Low temperatures results in more predictable text.
# Higher temperatures results in more surprising text.
# Experiment to find the best setting.
temperature = .1
# Here batch size == 1
for i in range(num_generate):
predictions = model(input_eval)
# remove the batch dimension
predictions = tf.squeeze(predictions, 0)
# using a categorical distribution to predict the character returned by the model
predictions = predictions / temperature
predicted_id = tf.random.categorical(predictions, num_samples=1)[-1,0].numpy()
# We pass the predicted character as the next input to the model
# along with the previous hidden state
input_eval = tf.expand_dims([predicted_id], 0)
chords.append(predicted_id)
return decode(chords)
starter = 'C^7'
print(tokenizer.word_index[starter])
generated = [generate_chord(model, start=tokenizer.word_index[starter]) for i in range(100)]25generated_encoded = [encode_chords(c) for c in generated]
generated_25s = [count25s(c) for c in generated_encoded]
print('Average number of 25 chord progressions', sum(generated_25s) / len(generated_25s))Average number of 25 chord progressions 4.03Conclusion
In conclusion, we’ve taken the series of songs, and built an LSTM model that can produce new chords. By utilizing jazz music theory know-how, we are able to treat the data in a way that eases the learning process for the model. There are still a lot of improvements to be made in this particular model. The model could understand time by refactoring the LSTM model to be a multivariate model. We could also further improve our understanding of the model by implementing form detection to see if there is a general AABA form structure.